1.introduction

在日常写缓存的时候经常遇到可以使用双向链表的情况，而这恰恰中了go的list包下怀。也许list包已经用的熟练了，但是这种强劲数据结构不免引人想去看看官方是怎么实现的。与此同时，我发现了这个包身边还伴随两个强劲的伙伴——ring和heap（环形链表和堆）。

他们统一都在container包中，接下来开始阅读。

2.list

众所周知list是一个双向链表。链表有节点，我们平时叫他“node”，但是在这里是一个叫element的结构

type Element struct {
	next, prev *Element
	list *List
	Value any
}

其中list很特殊，它代表一个list的容器。进一步说，是把一条双向链表给包装起来。这里的list指向“belongs to”

type List struct {
	root Element
	len  int     
}

这样一看就很明显了，一个链表有root（头一个元素），len（长度）。初步可以理解成这样

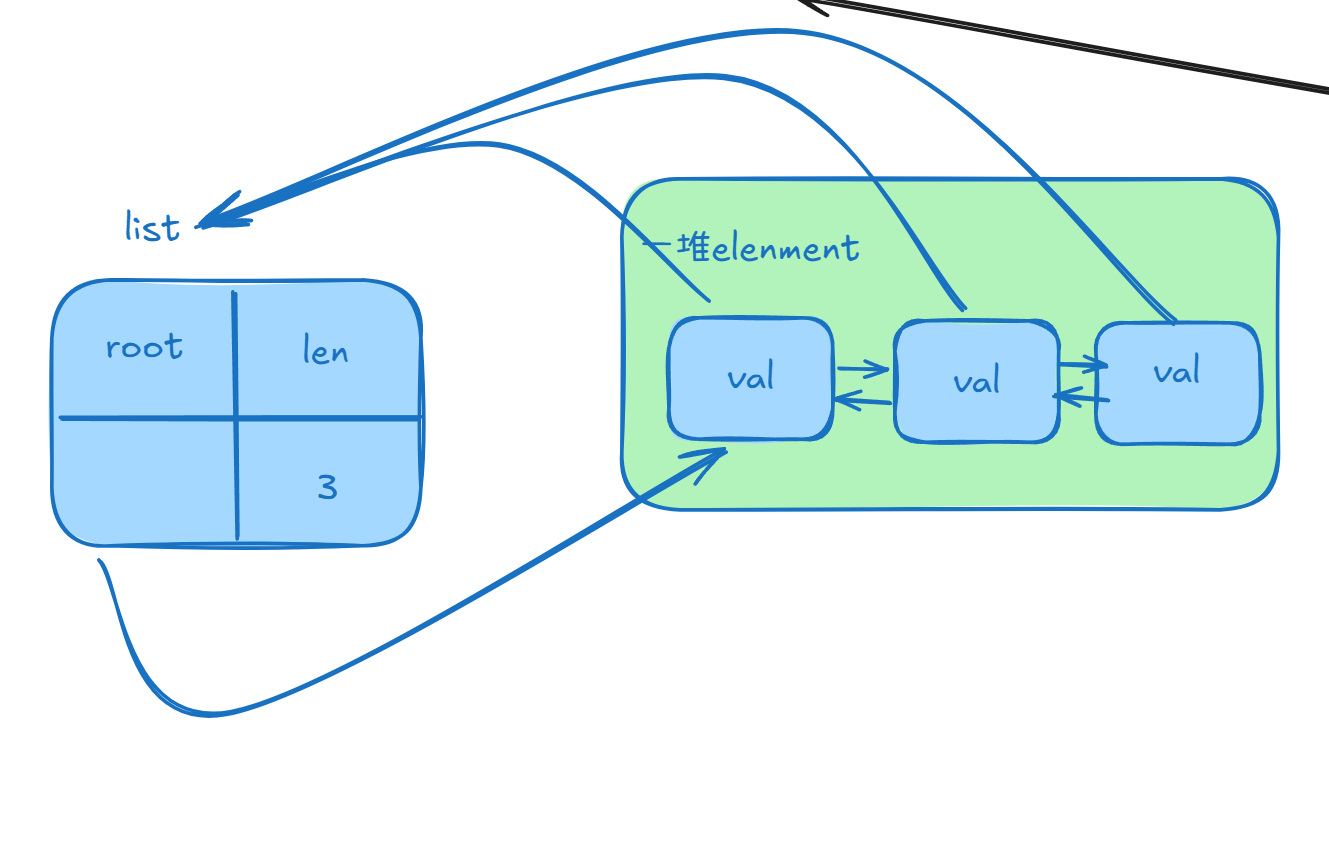
image-20250524230052736

神奇的一幕来了。我们之前认为New函数为非结构体函数，然而这里给出了一种诡异的思路。

// Init initializes or clears list l.
func (l *List) Init() *List {
	l.root.next = &l.root
	l.root.prev = &l.root
	l.len = 0
	return l
}

// New returns an initialized list.
func New() *List { return new(List).Init() }

也就是说，先用一个匿名的List调用Init方法，然后再进行返回。虽然如此，但是最终暴露给外界的也是一个非结构体函数。

可能只是google程序员脑洞做的一种尝试吧。总之达到的结果似乎没什么值得惊叹的地方。

剩下的方法就是对于头、尾中间的CRUD。

3.ring

环，没有特别可说的地方。注意它的next指的是“前进方向”。他的节点叫ring。

type Ring struct {
	next, prev *Ring
	Value      any // for use by client; untouched by this library
}

我们来讲讲一些特别的方法。

// Move moves n % r.Len() elements backward (n < 0) or forward (n >= 0)
// in the ring and returns that ring element. r must not be empty.
func (r *Ring) Move(n int) *Ring {
	if r.next == nil {
		return r.init()
	}
	switch {
	case n < 0:
		for ; n < 0; n++ {
			r = r.prev
		}
	case n > 0:
		for ; n > 0; n-- {
			r = r.next
		}
	}
	return r
}

Move，做旋转，假设前进方向为顺时针，n为正就顺时针，n为负就逆时针。

func (r *Ring) Link(s *Ring) *Ring {
	n := r.Next()
	if s != nil {
		p := s.Prev()
		r.next = s
		s.prev = r
		n.prev = p
		p.next = n
	}
	return n
}

对于Link（环的连接），我找到了很好的解析图。

对于不同的两个环：

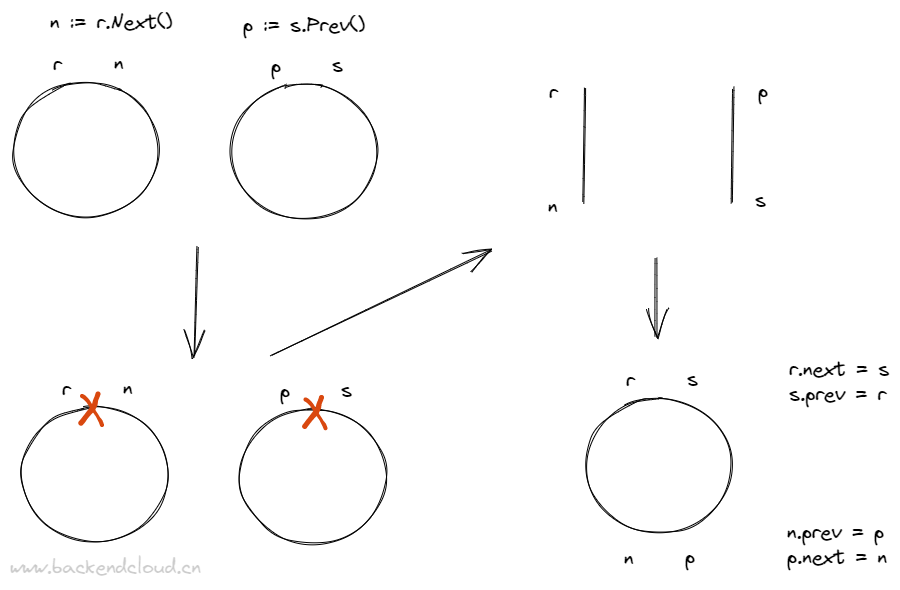
1748099729223

而对于同一个环上的两个节点则是去做拆分，则是做一个截取。

img

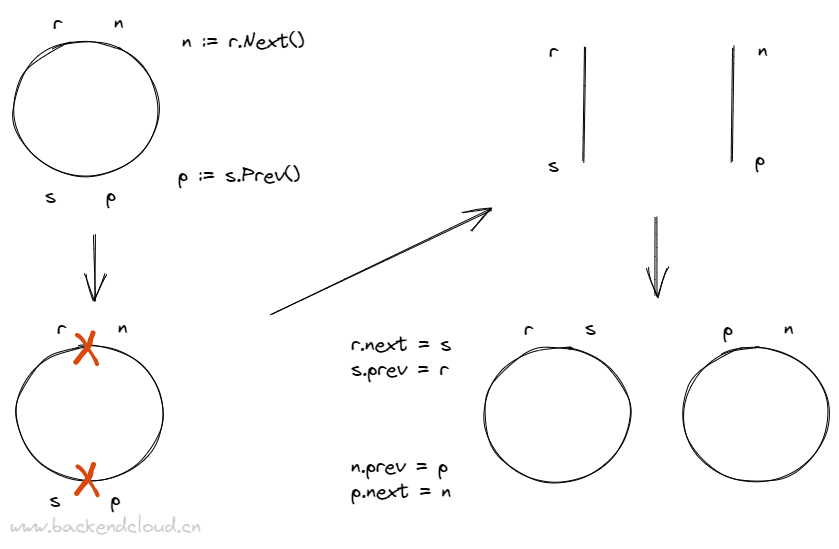
这个设计非常奇葩，首先就是在使用的时候，我们需要对返回的值是谁有清晰的认识。其次，我们需要认识清楚它是同一个环上的操作还是不同环上的操作。这要求对源码实现有深刻的理解。

总之，记住返回的是n，n之前一定是ρ。

func (r *Ring) Unlink(n int) *Ring {
	if n <= 0 {
		return nil
	}
	return r.Link(r.Move(n + 1))
}

unlink删除next开始的n个元素。这里的实现很有意思，用了link。也就是说同一个环，我保留r到r向前推进n+1之间的环。

func (r *Ring) Do(f func(any)) {
	if r != nil {
		f(r.Value)
		for p := r.Next(); p != r; p = p.next {
			f(p.Value)
		}
	}
}

Do，对于环上每个r，执行f(r)。

有什么使用场景呢？其实它最关键的特点是代表了一个双向链表首尾相连。所以我们要找收尾无延迟跳转的场景。

比如，循环队列。游戏里那种反复点击某个按钮进行装备切换这种操作。

固定大小循环缓冲区，比如我要保留多少大小的日志，那么达到容量老的就自动就被覆盖。

轮询调度，比如我们最近在设计网关的时候，就可以对某个服务的多个地址采取轮询调度的策略。

注：轮询调度（Round-Robin）是指按顺序逐个访问，而轮询（Polling）是指时间上周期性访问，不要混淆。

3.heap

heap留到最后，不仅因为它的场景关键，而且实现也复杂。

这个堆结构在container包特殊的地方在于，它提供了接口让开发者自己实现更多的扩展，而非直接提供了一个结构体。

先了解下sort包的接口。

type Interface interface {
	Len() int
	Less(i, j int) bool
	Swap(i, j int)
}

基本的排序，我们我们有比较和交换的环节。同时，遍历需要知道它的长度属性。

而heap的接口，继承sort的同时增加了push和pop

type Interface interface {
	sort.Interface
	Push(x any) // add x as element Len()
	Pop() any   // remove and return element Len() - 1.
}

目前我们可以认为，他是一个可排序的栈。对于可排序的栈（如优先队列）来说，我们不难想到这里的heap其实是一个数组，或者说slice的形式存在的。这与我们认知中的完全二叉树（节点实现）可能有一些出路。

在已有知识体系中，我们知道大小堆，而堆的排序叫做“下沉”。down返回bool代表该操作是否发生交换逻辑。

func down(h Interface, i0, n int) bool {
	i := i0
	for {
		j1 := 2*i + 1
		if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
			break
		}
		j := j1 // left child
		if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
			j = j2 // = 2*i + 2  // right child
		}
		if !h.Less(j, i) {
			break
		}
		h.Swap(i, j)
		i = j
	}
	return i > i0
}

这里可能需要解释一下。i0代表开始下沉的根。j1 := 2*i + 1中，j1代表i的左子节点，这是二叉树的特性。如果到这里你已经懵逼了，那我不得不画个图让你秒懂了。

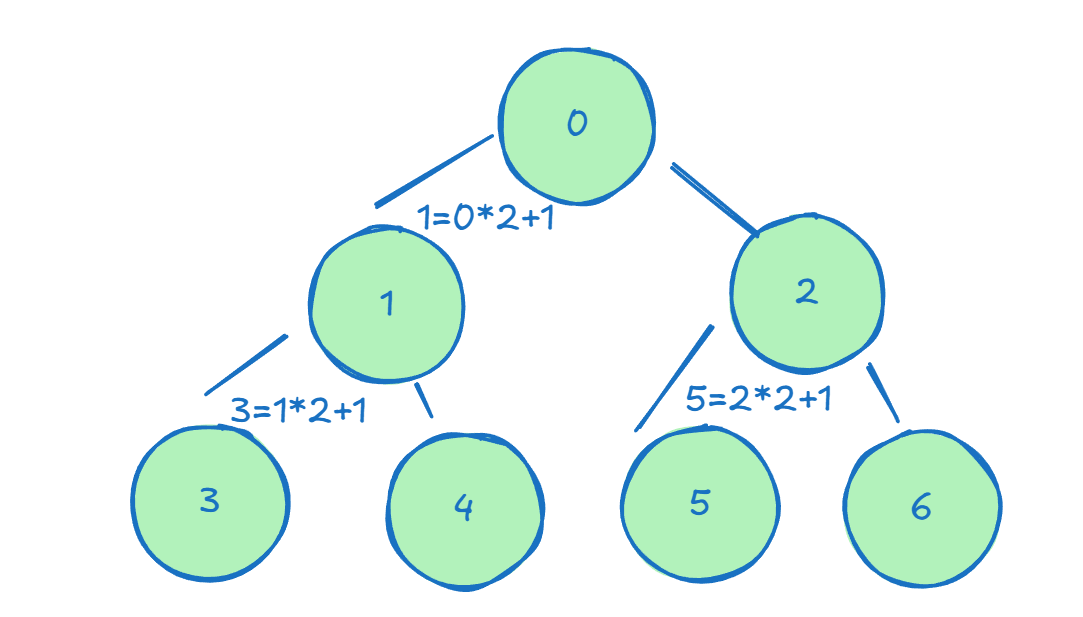
image-20250525002036945

没错，你已经懂了。那么显然，2*i+2就是右子节点。

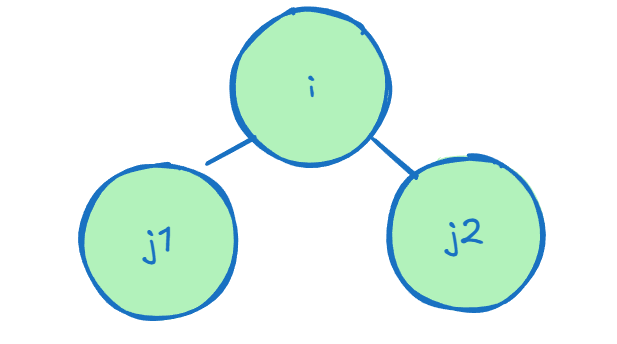
image-20250525002540471

上图是i，j1，j2的关系。假设less是判断左边参数更小，那么这就是一个小根堆，因为它找到了更小的值给了赋给了i。

接下来看初始化

func Init(h Interface) {
	// heapify
	n := h.Len()
	for i := n/2 - 1; i >= 0; i-- {
		down(h, i, n)
	}
}

也是一张图就可以看懂它是怎么构建出来一个小根堆的

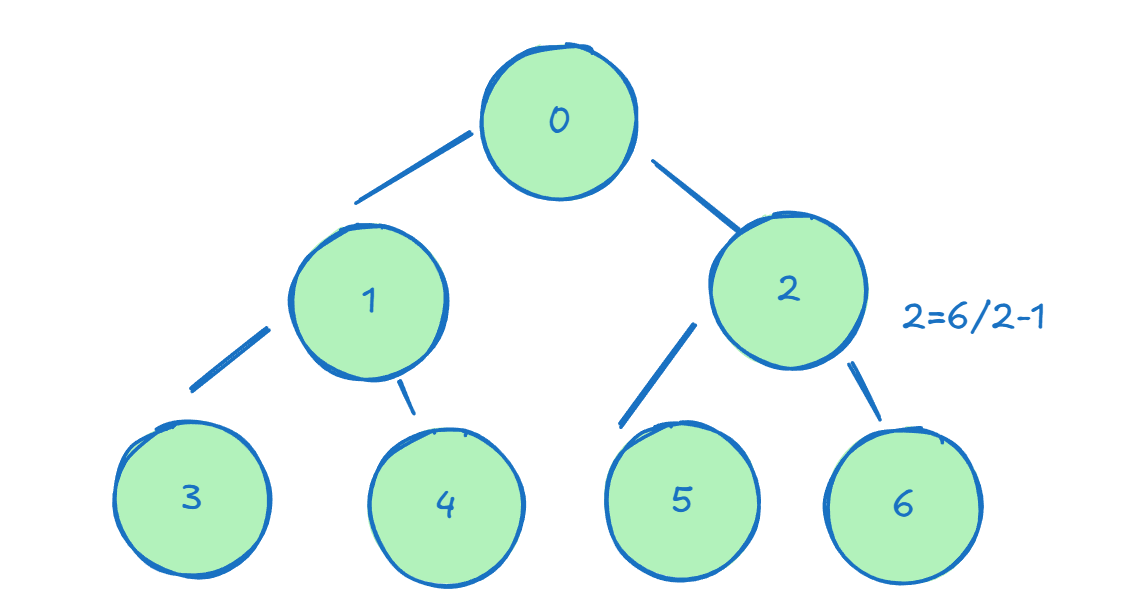
image-20250525003034946

然后看up是怎么做上浮的

func up(h Interface, j int) {
	for {
		i := (j - 1) / 2 // parent
		if i == j || !h.Less(j, i) {
			break
		}
		h.Swap(i, j)
		j = i
	}
}

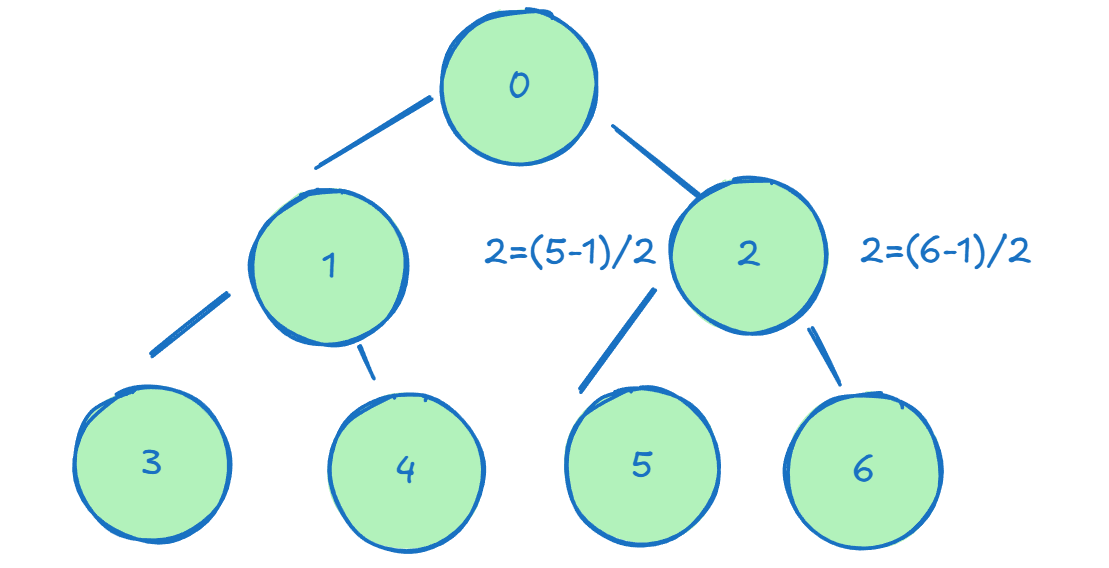
image-20250525003342746

无需多言。

heap由于是接口形式，因此它不可持有方法。我们采用非结构体函数形式存在。有了以上基础操作实现，heap包级函数实现将比较轻松。

func Push(h Interface, x any) {
    h.Push(x)
    up(h, h.Len()-1)
}

push（back）之后做上浮。

func Pop(h Interface) any {
    n := h.Len() - 1
    h.Swap(0, n)
    down(h, 0, n)
    return h.Pop()
}

pop（front）之后做下沉。

func Remove(h Interface, i int) any {
    n := h.Len() - 1
    if n != i {
       h.Swap(i, n)
       if !down(h, i, n) {
          up(h, i)
       }
    }
    return h.Pop()
}

移除操作，也是下沉。

func Fix(h Interface, i int) {
    if !down(h, i, h.Len()) {
       up(h, i)
    }
}

Fix，更改值之后重新建立秩序。它的开销会比remove之后再push小，因为是原地更改。

至此，实现一个优先队列进行练手。优先队列非常有用，比如经常用到的延时队列（超时、定时自动取消）就可以用它实现。

注：引自sdk的 container/heap/example_pq_test.go

// An Item is something we manage in a priority queue.
type Item struct {
    value    string // The value of the item; arbitrary.
    priority int    // The priority of the item in the queue.
    // The index is needed by update and is maintained by the heap.Interface methods.
    index int // The index of the item in the heap.
}

// A PriorityQueue implements heap.Interface and holds Items.
type PriorityQueue []*Item

func (pq PriorityQueue) Len() int { return len(pq) }

func (pq PriorityQueue) Less(i, j int) bool {
    // We want Pop to give us the highest, not lowest, priority so we use greater than here.
    return pq[i].priority > pq[j].priority
}

func (pq PriorityQueue) Swap(i, j int) {
    pq[i], pq[j] = pq[j], pq[i]
    pq[i].index = i
    pq[j].index = j
}

func (pq *PriorityQueue) Push(x any) {
    n := len(*pq)
    item := x.(*Item)
    item.index = n
    *pq = append(*pq, item)
}

func (pq *PriorityQueue) Pop() any {
    old := *pq
    n := len(old)
    item := old[n-1]
    old[n-1] = nil  // don't stop the GC from reclaiming the item eventually
    item.index = -1 // for safety
    *pq = old[0 : n-1]
    return item
}

// update modifies the priority and value of an Item in the queue.
func (pq *PriorityQueue) update(item *Item, value string, priority int) {
    item.value = value
    item.priority = priority
    heap.Fix(pq, item.index)
}

关键点：

1.index代表外界的下标，因此swap时候需要主动更新。

2.优先队列是大根堆，所以用大于号

3.update为修改值，也就是说支持动态调整，这是对于传统优先队列改进的地方。换句话说，它不是单一个可排序的栈，甚至可以修改值进行动态调整，这在生产环境中非常优越，比如我可以修改定时任务的值。

4.end

累了，毁灭吧。